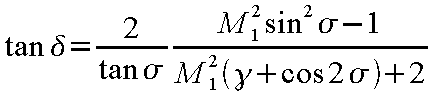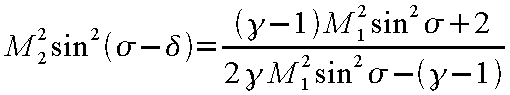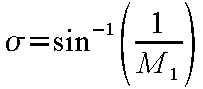●　斜め衝撃波

　　　凹角を有する壁面やくさび型の物体を過ぎる超音速流れでは、以下に示すような斜めに傾いた衝撃波を生ずる。
これを斜め衝撃波 (Oblique  shock wave) と呼んでいる［図中のＳＷ は衝撃波(Shock Wave)を示している］。

この斜め衝撃波は衝撃波面を基準として考えると、前述の垂直衝撃波と同様の性質を有している。
これを以下の図を用いて解説する。 

　いま、図において衝撃波発生前の速度を ｕ_１ 、発生後の速度を ｕ_２ とする。また、斜め衝撃波に対して
接線方向の成分をそれぞれ ｕ_１ｔ 、ｕ_２ｔ  とし、垂直方向の成分をそれぞれ ｕ_１ｎ 、ｕ_２ｎ とする。
図のように衝撃波によって影響を受ける（減速する）速度成分は垂直成分のみである。
また、衝撃波が発生するためにはｕ_１ｎ が超音速（Ｍ ＞１ ）でなければならず、
よって ｕ_１ はそれ以上の速さの超音速である。さらに、ｕ_２ｎ は衝撃波により亜音速（Ｍ ＜１ ）に減ずるが、
ｕ_２ は必ずしも亜音速でないことに注意しなければならない。実際にｕ_２ は超音速であることが多い。

　　斜め衝撃波後の流れは超音速であることが多い。

　ここで、上図に示された速度成分の関係をまとめると

(12-34)

である。また、接線成分は影響を受けないため

(12-35)

となり、垂直成分の関係は

(12-36)

と表される。この式をランキン・ユゴニオの式に代入して
［式（12-30）のｕ_１ ／ｕ_２  を ｕ_１ｎ ／ｕ_２ｎ  に、式（12-31）の上流側マッハ数Ｍ _１ をＭ _１ ｓｉｎσに置き換える］整理すると

(12-37)

の関係が得られる。

また、加えて式（12-33）の下流側マッハ数Ｍ _２ をＭ _２ ｓｉｎ（σ−δ）に置き換えると

(12-38)

が求まる。
　

　　●　付着衝撃波を利用したマッハ数計測

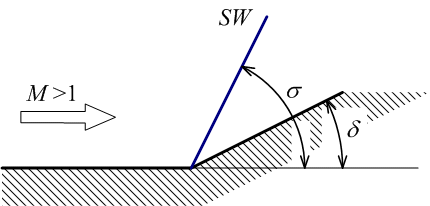
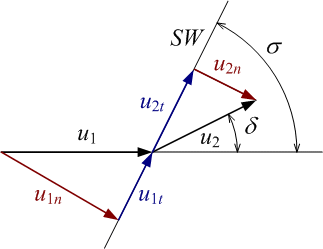
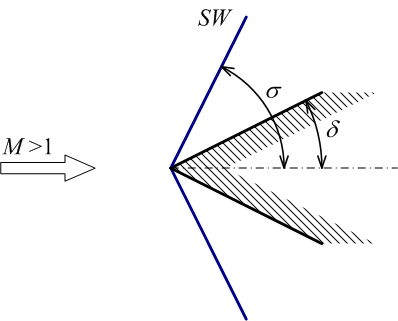
　下図のような半頂角δが既知のくさび型物体を超音速流中に挿入すると、
傾き角σの斜め衝撃波が発生する。この衝撃波は、物体の先端に付着したものであるため
付着衝撃波と呼ばれる。
よって、σを測定することによって式(12-37)から衝撃波発生前の
マッハ数Ｍ _１ を求めることができる。ただし、Ｍ _１ を算出するにはコンピュータの支援が必要である。
また、同様に式(12-38)から衝撃波発生後のマッハ数Ｍ _２ を計算できる。

　ここで、δを固定して式(12-37)を考察すると、σが求まるＭ _１ には下限があることがわかる。
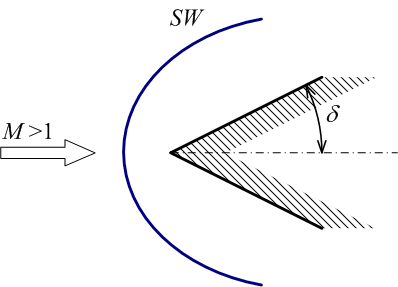
この下限を下回ったＭ _１ では付着衝撃波となることができず、下図のような
物体から衝撃波が離れた離脱衝撃波となる。

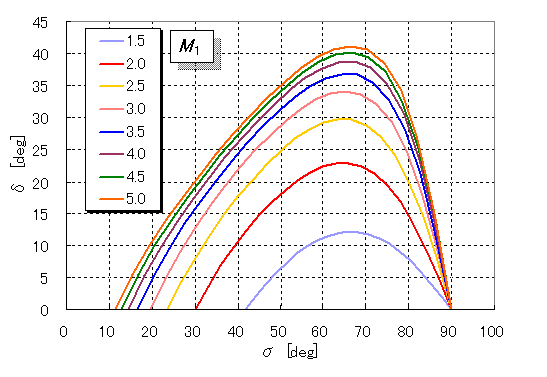
　また、同様にＭ _１ を固定して（パラメータとして）式(12-37)を考察すると、以下のグラフのような曲線が得られる。

　図のようにσの上限はＭ _１ によらず90°であるが、下限はマッハ角と同じ

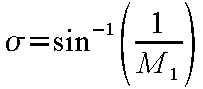(12-39)

となる。
　図より、各マッハ数において、δの最大値であるδ_max の存在が確認でき、
このδ_max より上の値のもつδではσが求まらないことがわかる。（δ＝δ_max である場合、Ｍ _２ ＝ １ となる。）
よって、δ_max ＜δである場合、離脱衝撃波となる。また、δ_max ＞δである場合、σは２種類の値を持つ。
δ_maxにおけるσをσ_mとすれば、σ＜σ_mの場合にはＭ _２ ＞ １ となり、逆にσ＞σ_mの場合にＭ _２ ＜１ となる。
Ｍ _２ ＞ １の場合を弱い衝撃波、Ｍ _２ ＜１の場合を強い衝撃波と呼んでいる。
この弱い・強い衝撃波のうち、どちらが発生するかは上流と下流の圧力に依存する。
一般に、下流／上流の圧力比が小さい方の弱い衝撃波が発生することが多い。
このことからも斜め衝撃波後の流れは超音速であることが多いといえる。
　なお、円形のような鈍頭物体の場合にはδが90°であり、
Ｍ _１ によらずδ_max よりも大きいため常に離脱衝撃波となる。

　○　以下にくさびによるマッハ数測定の計算表示プログラムのリンクを示す。
　　　ファイルには、半頂角δの計算および付着・離脱衝撃波の判定も含まれている。
　　
　くさびによるマッハ数測定の計算プログラム［表計算ファイルのダウンロード］

　表計算ファイルの各タブで計算を行う。

→　戻る