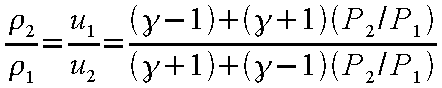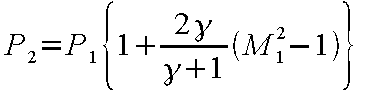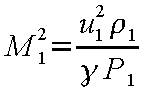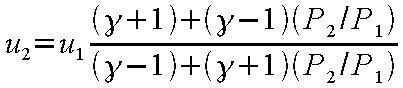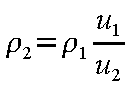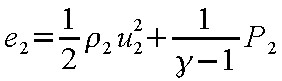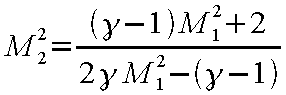|
● 垂直衝撃波
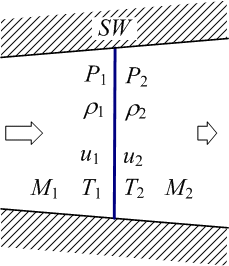
以下の図に示しているラバルノズルの末広部で発生するような流れ方向に垂直な衝撃波を
垂直衝撃波 (Normal shock wave) と呼んでいる[図中のSW
は衝撃波(Shock Wave)を示している]。
この垂直衝撃波の厚さは非常に薄いため、衝撃波発生前後の管断面積は同一と考えることができる。
また、衝撃波が発生する流れにおいても式(12-5)〜式(12-7)の関係が成り立つ。
(ただし、各物理量は衝撃波発生前後で不連続であり、等エントロピー流れとはならない。)
これら3つの式を連立させると
|
|
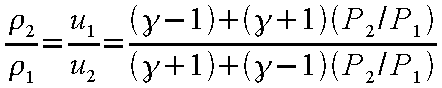 |
(12-30) |
|
|
なる関係が得られる(発生前:点1、発生後:点2)。これをランキン・ユゴニオ(Rankine-Hugoniot)の式と呼んでいる。
また、衝撃波発生上流のマッハ数は必ず1以上であり、衝撃波の発生によって
エントロピーは増大する。よって、衝撃波を伴う流れは非等エントロピー流れでもある。
まとめると、衝撃波が発生する場合、P 1<P
2 、 ρ 1<ρ2 、u 1>u
2 、T 1<T2 となる。
すなわち、圧力、密度、温度は増大し、速度(マッハ数)は減少する。
この垂直衝撃波の関係式を式(12-30)の形で表すよりも以下に示すような上流側マッハ数M 1
を用いた表示が便利である。
|
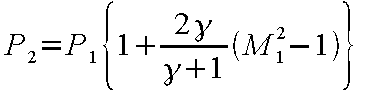 |
|
(12-31) |
|
|
ここで、M 1
が未知の場合は次の式で計算できる。
|
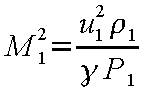 |
|
(12-32) |
|
|
よって、上流側の値からP
2 が求まるため、順次、下流側の諸量を計算することができる。
|
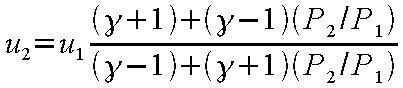 |
|
(12-33) |
|
|
|
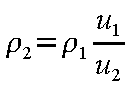 |
|
(12-34) |
|
|
|
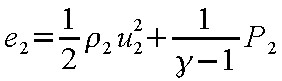 |
|
(12-35) |
|
|
なお、下流側マッハ数M 2 は、
|
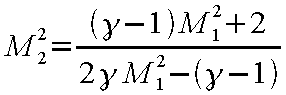 |
|
(12-36) |
|
|
で求まる。
○ 以下に拡大管内の垂直衝撃波計算プログラムのリンクを示す。
拡大管内垂直衝撃波計算プログラム[表計算ファイルのダウンロード]
垂直衝撃波の発生位置は固定されているので断面積の変化に対する出口圧力の変化を調べる。
なお、垂直衝撃波の発生位置は計算上の管長さの半分の位置であり、拡大管はラバルノズルの末広部を
想定している。したがって、入口速度を音速とする。
|