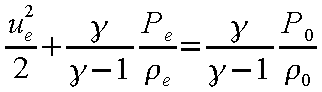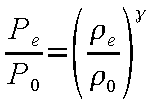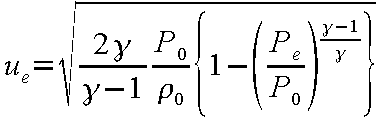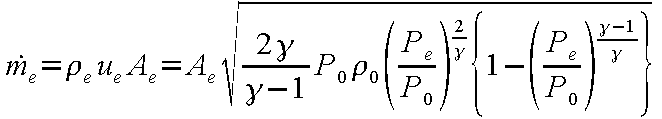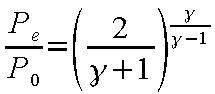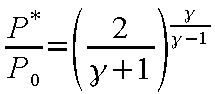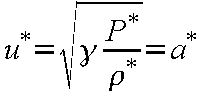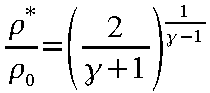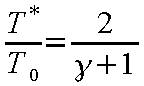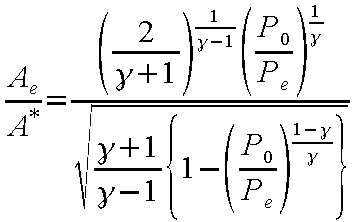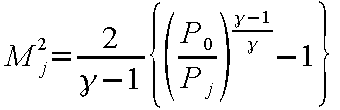●　先細ノズル

　　　既に１次元流れにおいて学んだように亜音速流において流れを加速させるには
　管断面積を流れ方向に小さくする（絞る）必要がある。
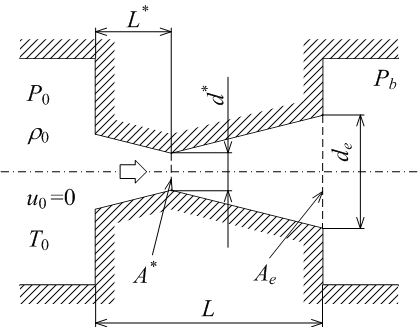
　　いま、流れ方向に管断面積が小さくなるノズル（nozzle、流れを加速させる流路）内の流れを考え、その概略を下図に示す。
［※　ノズルに対して逆に流れを減速させる流路を一般にディフューザ（diffuser）という。］

   図においてノズル部は長さ Ｌ をとる部分である。
また、ノズルに接続したタンクは上流側、下流側ともにノズルに比べて極めてに大きいと仮定する。
この流路のように流れ方向に断面積が小さくなっていくノズルを先細ノズル（convergent nozzle）と呼んでいる。
　この先細ノズルに関する流れを定常１次元圧縮性流れを用いて考察してみる。
ノズルは実際には軸対称形（断面が円形）のものが多いが１次元流れを考える際には２次元形状を仮定してもよい。
いま、ノズル上流のタンク内でよどみ状態（ｕ _０＝０）、全ての壁面で断熱を仮定し、流体の粘性は考慮しないことにする。
ノズル下流のタンク内圧力［背圧 (Back pressure) という］の初期値をＰ _ｂ ＝Ｐ _０ とすれば、
この段階で流れは生じない。また、ノズル出口圧力Ｐ_ｅ もＰ_ｅ ＝Ｐ _ｂ である。
ここから、Ｐ _ｂ ＜Ｐ _０にすると流れが発生する。
流れが亜音速である場合、圧力差（Ｐ _０−Ｐ _ｂ ）で流量（すなわち、流速も）が決まり、ノズル出口圧力Ｐ_ｅ はＰ_ｅ ＝Ｐ _ｂ のままである。
　さらに、Ｐ _ｂ を減少させていくと、下流のタンクに排出するノズル出口流速が音速（Ｍ  ＝ １ ）に達する。
さて、前述したように音速を越えた超音速状態では、流れ方向に流路断面積が小さくなっていくと
速度が減少する。すなわち、この先細ノズルを用いると、音速に達した背圧からさらに圧力を減少させても
ノズル出口流速が音速を越えることができないのである。
  上の考察を式を用いて示すと、まず、よどみ状態のタンクとノズル出口間の流れの関係式は等エントロピー流れを仮定して

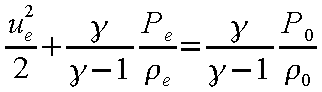(12-17)

となり、さらに

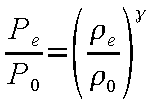(12-18)

を用いてρ_ｅ を消去した後、ノズル出口流速 ｕ_ｅ について解くと、

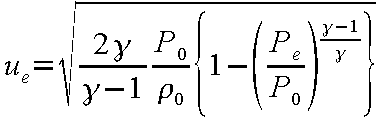(12-19)

を得る。また、この流速からノズル出口質量流量は、

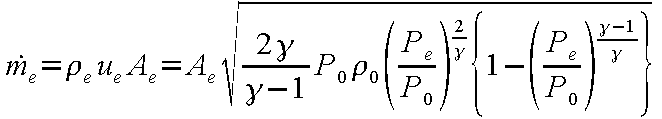(12-20)

となる。ここで、ノズル出口圧力とよどみ点圧力の比 Ｐ_ｅ ／Ｐ _０を関数として、式（12-20）によって計算される
ノズル出口質量流量を考察すると、この比が

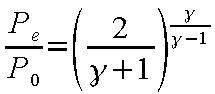(12-21)

のときに最大値を示す。このノズル出口圧力を臨界圧力 Ｐ^＊ と呼ぶ。
（臨界状態の物理量にアスタリスク＊を付加する。別の頁の表現と混同しないように注意する。）
式（12-21）を臨界圧力 Ｐ^＊ で書き換えると

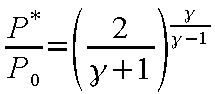(12-22)

となる。この式（12-22）の関係を式（12-19）に適用すると、臨界速度ｕ^＊ は

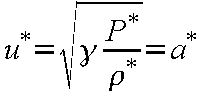(12-23)

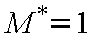(12-24)

であることがわかる。すなわち、 臨界速度ｕ^＊ は音速であり、マッハ数 Ｍ^＊  ＝ １ となる。
この臨界圧力 Ｐ^＊ より背圧Ｐ _ｂ を減少させても出口圧力は Ｐ_ｅ ＝Ｐ^＊  （Ｐ _ｂ ＜Ｐ_ｅ ）であり、出口質量流量も変化しない。
これを流れがチョーク（閉塞）した状態と呼んでいる。
また、臨界密度ρ^＊ と臨界温度Ｔ^＊ はそれぞれ

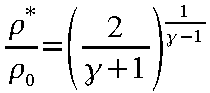(12-25)

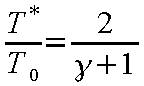(12-26)

の関係で表される。

　先細ノズルに関する計算演習［表計算ファイルのダウンロード］

　背圧Ｐ _ｂ を変化させたときの諸量の変化を演習する。
　

　　●　ラバルノズル

　　　前で述べたように先細ノズルでは、その出口で超音速流を生成することはできない。
　静止流体（亜音速流）から超音速流を生成するには先細末広ノズル（convergent-divergent nozzle、中細ノズルともいう）を
　用いる必要がある。
　また、このノズルは最初に実用化したスウェーデンの技術者、ラバルの名前からラバルノズル(Laval nozzle)とも呼ばれている。
　　
　　はじめにこのラバルノズルに関する流れを定常１次元圧縮性流れを用いて考察してみる。
以下にラバルノズルに関する流れの概略を示す。

   図においてノズル部は長さ Ｌ をとる部分である。
また、ノズルに接続したタンクは上流側、下流側ともにノズルに比べて極めてに大きいと仮定する。
このノズル部において最も管断面積が小さい部分をスロート（throat、のど部）という。
図からわかるようにこのスロート位置までは先細ノズルと同様の形状を示しており、この先細部では
先細ノズルの性質を持っている。よって、先細ノズルの解説で述べたようにラバルノズルにおいてもこのスロート位置で
流れがチョークすることがある。このため、便宜上、スロートに関わる物理量にアスタリスク＊を付加した。
一方、スロート下流からタンクまでの部分を末広部という。
　いま、ノズル下流のタンク内背圧の初期値をＰ _ｂ ＝Ｐ _０ とすれば、この段階で流れは生じない。
ここから、Ｐ _ｂ ＜Ｐ _０にすると流れが発生する。
さらに、Ｐ _ｂ を減少させていきスロート位置の圧力が臨界圧力に達すると、スロート位置で流れがチョークする。
この最初にチョークに達したノズル出口圧力Ｐ _ｄ ＝Ｐ _ｅ では流れは末広部で亜音速になる。
一方、これよりも下げたあるノズル出口圧力Ｐ _ｊ ＝Ｐ _ｅ 以下では末広部で超音速流れを維持できる。
これらのノズル出口圧力Ｐ _ｄ  ，Ｐ _ｊ は、後述するようにスロート断面積とノズル出口断面積の比で一様に求まる。
なお、この中間に位置するノズル出口圧力Ｐ _ｄ ＞Ｐ _ｅ＞Ｐ _ｊ  における流れの挙動はさらに
後述する衝撃波がノズル出口位置で発生する圧力Ｐ_ｈ によって区分される。
すなわち、Ｐ _ｄ ＞Ｐ _ｂ＞Ｐ _ｈ  では衝撃波が末広部に発生し、そのため流れはその下流で亜音速に減ずる。
一方、Ｐ _ｈ＞Ｐ _ｂ＞Ｐ _ｊ   ではノズル出口での状態が過膨張(over-expansion)状態と呼ばれる。
さらに、Ｐ _ｈ＞Ｐ _ｂ のノズル出口での状態を不足膨張(under-expansion)状態という。
　ノズル出口圧力Ｐ _ｊ ＝Ｐ _ｅ では超音速流れを維持でき、ラバルノズルにおける目的の作動状態であるため、
適正膨張(correct expansion)の状態と呼んでいる。
　さて、この適正膨張時のノズル出口圧力Ｐ _ｊ ＝Ｐ _ｅ と最初にチョークに達したノズル出口圧力Ｐ _ｄ ＝Ｐ _ｅ は
以下の計算式で求まる。

(12-27)

ここで、Ａ _ｅ ／Ａ^＊ は出口とスロート断面積の比である。
なお、Ａ _ｅ ／Ａ^＊ を用いて Ｐ _ｄ  ，Ｐ _ｊ を求めることは計算が難しいため、Ｐ _０／Ｐ_ｅ を変化させてＡ _ｅ ／Ａ^＊ を求め、
その表を作成しておくと都合がよい。
　また、衝撃波がノズル出口位置で発生する場合の出口圧力Ｐ_ｈ は以下の式で示される。
ノズル出口位置で衝撃波が発生する場合には、その直前の圧力はＰ _ｊ であり、そのときの
マッハ数M _ｊ を用いて計算できる。

(12-28)

(12-29)

　ラバルノズルに関する計算演習［表計算ファイルのダウンロード］

　背圧 Ｐ_ｂ  、出口断面積 Ａ_ｅ  を変化させたときの諸量の変化を演習する。

● ラバルノズル流れの背圧によるまとめ

   (1)  Ｐ _ｂ＝ Ｐ _ｅ ＝Ｐ _０ 　　　　　　：　流れなし
 　(2)　Ｐ _ｄ  ＜Ｐ _ｂ ＝ Ｐ _ｅ ＜Ｐ _０：　全体で亜音速流れ
　 (3)　Ｐ _ｂ＝ Ｐ _ｅ ＝Ｐ _ｄ：　スロートで音速、末広部で亜音速
    (4)　Ｐ _ｈ ＜Ｐ _ｂ ＝ Ｐ _ｅ ＜Ｐ _ｄ：　末広部で衝撃波
　 (5)　Ｐ _ｈ ＝Ｐ _ｂ ＝ Ｐ _ｅ ：　ノズル出口で衝撃波
　 (6)　Ｐ _ｊ ＝ Ｐ _ｅ ＜Ｐ _ｂ ＜Ｐ _ｈ ：　過膨張　　 （　 Ｐ_ｅ ／Ｐ _ｂ　＜１ ）
　 (7)  Ｐ _ｂ＝ Ｐ _ｅ ＝Ｐ _ｊ            ：　適正膨張　（　 Ｐ_ｅ ／Ｐ _ｂ　＝ １ ）
　 (8)  Ｐ _ｂ　＜Ｐ _ｊ ＝ Ｐ _ｅ           ：　不足膨張　（　 Ｐ_ｅ ／Ｐ _ｂ　＞ １ ）

　Ｐ _ｂ：　背圧
　Ｐ _ｅ 　：　ノズル出口圧力

　Ｐ _０ 　：　全圧
　Ｐ _ｄ：　スロートで音速、末広部で亜音速となる圧力
　Ｐ _ｈ：　ノズル出口で衝撃波を生じる圧力
　Ｐ _ｊ：　適正膨張となる圧力

　

→　戻る