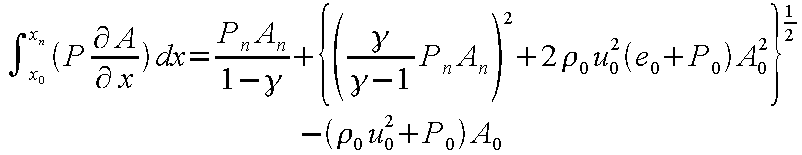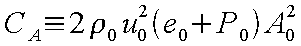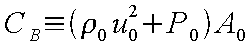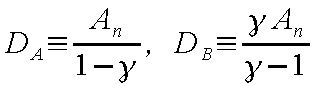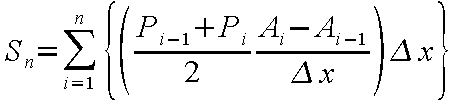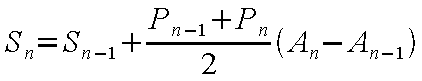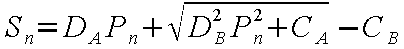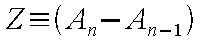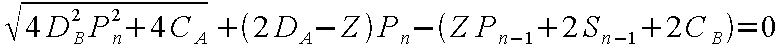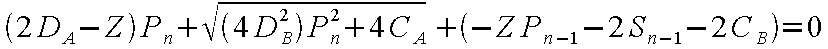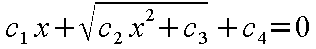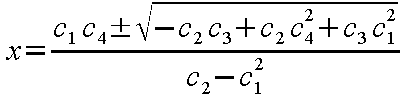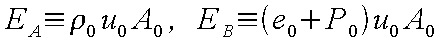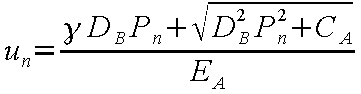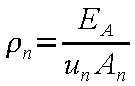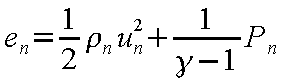|
● 管断面積が変化する定常1次元圧縮性流れの計算例
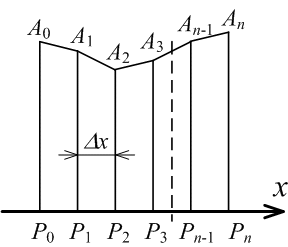
管路の断面積が変化する定常1次元圧縮性流れに関する座標を以下に示す。
|
|
 |
|
|
|
|
|
座標の定義 |
|
|
|
上の図に基づき、式(12-3)
を
のように書き換える。ここで、
とおく。
一方、図に従って式(12-3)の左辺を簡易的に数値積分する式は
と表され、いま、Sn
を求めるに際し、 Sn−1 、Pn−1
が既知であると仮定すると
(An−1 は流路の形状であるため既知)
と示すことができる。また、右辺は上記定義より
で表される。、さらに、ここで
とおく。これらから、基礎式は
となり、これを並べ替えて
を得る。一方、

|
以下の方程式
の解は
となる。
|
|
よって、Pn
を求めることができる。Pn
の値は上式に”±”があるため2つ存在する。
この”±”は流れが、亜音速か超音速かで異なり、亜音速であれば”+”、超音速であれば”−”で計算する。
得られたPn
から順次
が計算できる。
定常1次元圧縮性流れに関する演習[表計算ファイルのダウンロード]
速度を亜音速(1未満の値)、超音速(1より上の値)と変化させる。
また、断面積変化用定数を+0.001や−0.001といった値に変更し、管断面積を拡大、収縮方向に変化させる。
変更により各値がリアルタイムに再計算される。
なお、本計算では亜音速と超音速をまたぐ流れは計算できないので注意する。
|