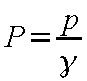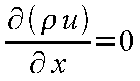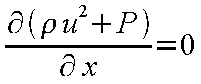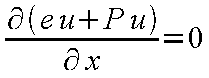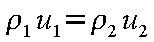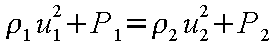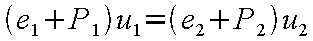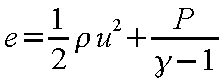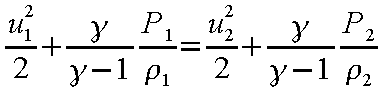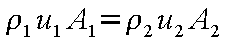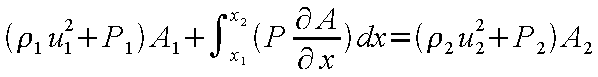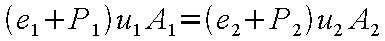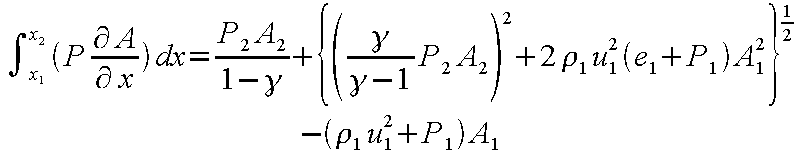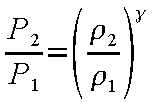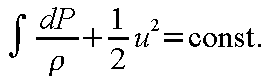|
● 定常1次元圧縮性流れ
圧縮性流れの基礎として粘性を無視した定常1次元圧縮性流れについて考察を行う。
この流れを表す無次元基礎方程式(本講義では数値解析結果との比較を容易とするため無次元化された式群を用いる)は
2次元圧縮粘性流れにおける無次元化支配方程式 (ブラウザの”戻る”で戻ること)
から導くことができるが、ここでは、次元量の式と無次元化式でみかけ上の表示を同一とするため
|
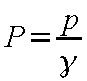 |
|
(12-1) |
|
|
なる無次元圧力を導入する。2次元圧縮粘性流れの式に対して時間および粘性に関する項、y 方向運動方程式、
y 方向速度成分v に関する項が消去される。
よって、以下の3つの偏微分方程式(連続の式、運動方程式、エネルギー方程式)が得られる。
|
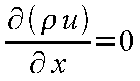 |
|
(12-2) |
|
|
|
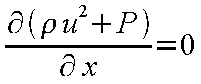 |
|
(12-3) |
|
|
|
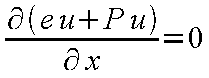 |
|
(12-4) |
|
|
いま、管内の流れを考え、管の断面積が一定、管壁で断熱を仮定すると式(12-2)〜式(12-4)よりx
方向の点1および2のつりあいの式
|
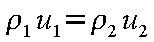 |
|
(12-5) |
|
|
|
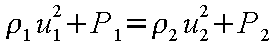 |
|
(12-6) |
|
|
|
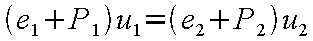 |
|
(12-7) |
|
|
が得られる。
ここで、
|
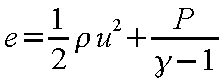 |
|
(12-8) |
|
|
であるため、式(12-7)は以下のようにも表せる。
|
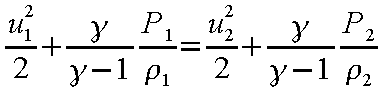 |
|
(12-9) |
|
|
式(12-9)は、非圧縮性流体におけるベルヌーイの式に相当する。
さらに、管の断面積 A
が変化する場合を考えると x
方向の点1および2のつりあいの式は
|
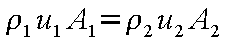 |
|
(12-10) |
|
|
|
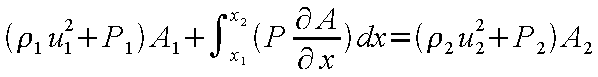 |
|
(12-11) |
|
|
|
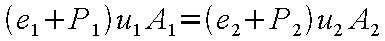 |
|
(12-12) |
|
|
のように表せる。ここで、積分記号中の P 、A
は x
方向の位置によって変化する変数である。
いま、式(12-10)〜式(12-12)において点1における諸量を既知と仮定して整理すると圧力のみが
未知である以下の式を得る。
|
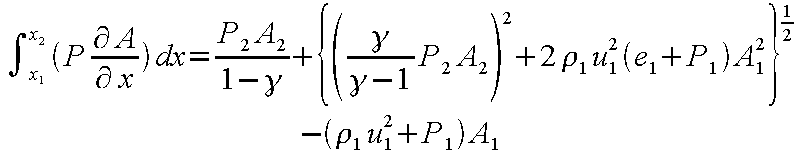 |
|
(12-13) |
|
|
なお、式(12-13)のA 2は管路の断面積であるので既知である。式(12-13)のP
2が得られれば代数計算によって
ρ2、u 2を得ることができる。ただし、この計算は複雑であるためコンピュータの支援を必要とする。
|