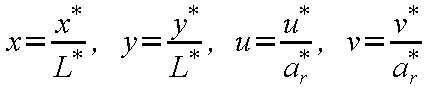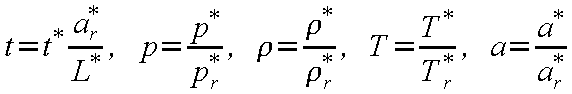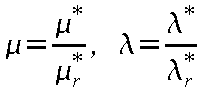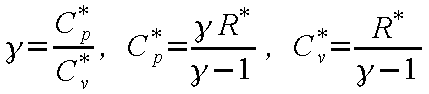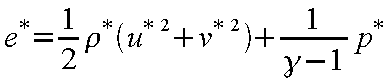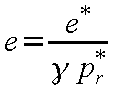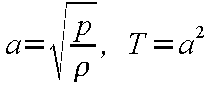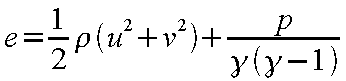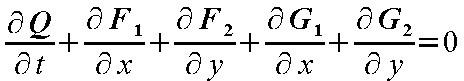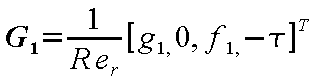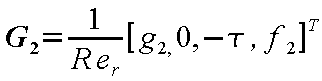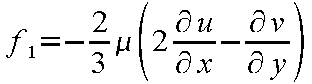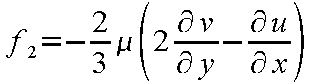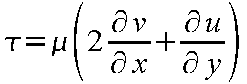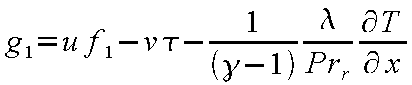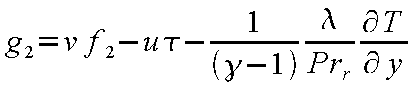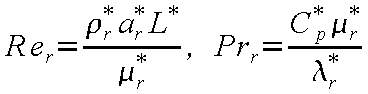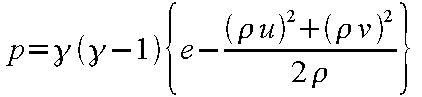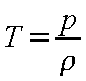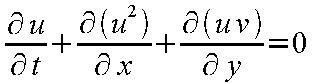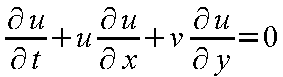|
● 2次元圧縮粘性流れにおける無次元化支配方程式
2次元圧縮粘性流れにおける支配方程式(NS方程式)は、
エネルギー方程式、連続の式、x 方向運動方程式、y 方向運動方程式からなる。
さらに温度を決定するために状態方程式を導入する。
無次元化された支配方程式を保存型(conservative
form)*1のベクトル形式で表示すると
|
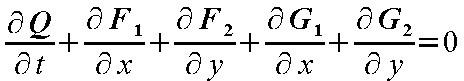 |
|
(24-13) |
|
|
となる。ここで、Q
は従属変数*2ベクトル、F 1
および F 2
は非粘性流束ベクトル、
G 1 および G 2
は粘性流束ベクトルを表している。
その各ベクトル成分は
|
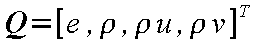 |
|
(24-14) |
|
|
|
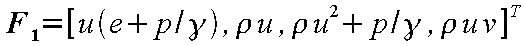 |
|
(24-15) |
|
|
|
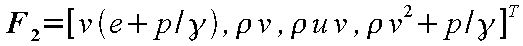 |
|
(24-16) |
|
|
|
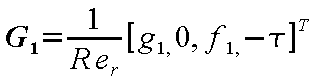 |
|
(24-17) |
|
|
|
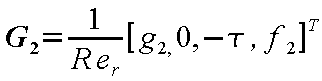 |
|
(24-18) |
|
|
と表せる。また、
|
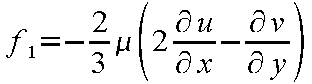 |
|
(24-19) |
|
|
|
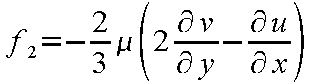 |
|
(24-20) |
|
|
|
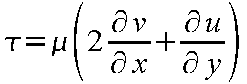 |
|
(24-21) |
|
|
|
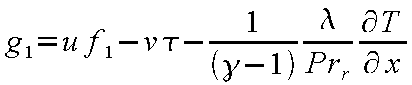 |
|
(24-22) |
|
|
|
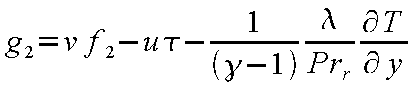 |
|
(24-23) |
|
|
である。さらに、レイノルズ数
Rer 、プラントル数 Prr
は
|
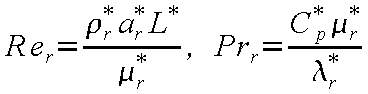 |
|
(24-24) |
|
|
で示される。
また、圧力p
は式(24-12)から
|
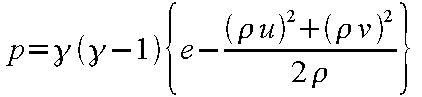 |
|
(24-25) |
|
|
となり、温度T
は式(24-11)[状態方程式]から
|
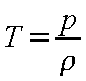 |
|
(24-26) |
|
|
である。
なお、従属ベクトルという用語からも察することができるように、本方程式(24-13)を解いて直接得られる
値は、 密度 ρ 、 x 方向質量速度 ρu 、
y 方向質量速度 ρv 、
単位体積あたりの全エネルギー e である。
各計算点でこれらの値が求まれば、その点での圧力、温度などが計算できる。
また、粘性に関する項を省略すれば、上記NS方程式はオイラー方程式となる。
*1 : 保存型方程式
物理量が全て微分記号の中で示されている方程式。
例えば、保存型方程式は
であり、非保存型方程式は
と表せる。両者は数学的には同じ(連続の式を導入した場合)であるが、差分表示では異なる計算結果となる。
圧縮性流体計算では、一般に保存型表示が用いられる。
*2 : 独立変数と従属変数
y = f( x ) における x
はその値を自由に設定できる。一方、y は x
の関数となっており、
x
の値によって変化する。この x
のような変数を独立変数、y のような変数を従属変数と呼んでいる。
|