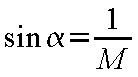|
● 音波の伝播
周囲の流れ(流速)によって音波の伝わり方、すなわち、伝播(でんぱ)の仕方は異なる。
以下に音源と流れ方向および座標の定義を示す。
|
|
 |
|
|
|
|
|
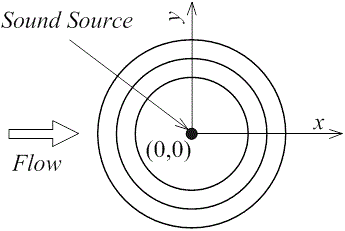
音源と流れ方向および座標の定義 |
|
|
|
音源を原点[0,0]として、x
軸方向に 平行な流れが左から右に
マッハ数 M
で流れると仮定する。
まず、静止流体中を考えると、音は微小な圧力変動であり、音源から全ての方向に音速
a で伝播する。
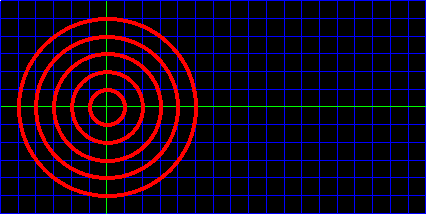
下図において、緑線は軸線であり、音源はその交点にある。
また、赤線は、ある時間刻みごとの伝播位置を示す円である(以降も同様)。
|
|
 |
|
|
|
|
|
静止流体中における音波の伝播 |
|
|
|
次に、M
<1の流れがある場合、すなわち亜音速流を考えると、音波面は上流側に
(1−M )の速度で伝わり、
下流側には(1+M )の速度で伝播する。これを図に示すと、
|
|
 |
|
|
|
|
|
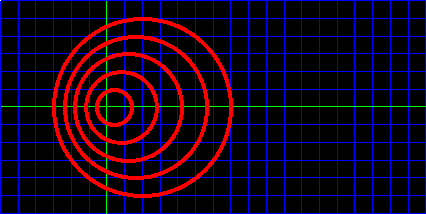
亜音速流中(M
<1)における音波の伝播 |
|
|
|
となり、波面の間隔は上流側で密となり、下流側で疎となる。
ここで、観測者が流れとともに M
で移動すると上流側で高音、下流側で低音に音が歪む。
これは、ドップラー効果である。
また、M
=1(音速流)の場合を考えると、以下のようになり、
|
|
 |
|
|
|
|
|
音速流中(M
=1)における音波の伝播 |
|
|
|
音波は音源より上流には伝わらなくなる。この場合の音波面をつないでいくと
音源の点を含む流れに垂直な面(図で黄色の線)が形成される。
これをマッハ波 (Mach wave) と呼んでいる。
さらに、M
>1(超音速流)の場合は、
|
|
 |
|
|
|
|
|
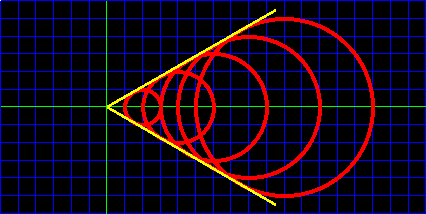
超音速流中(M
>1)における音波の伝播 |
|
|
|
となり、音波面は下流に流されていく。これらの音波面で形成される面(図中の黄色の線)は
円錐状となる。これをマッハ円錐(マッハコーン)
(Mach cone) という。
音はこのマッハ円錐内でのみ伝播する。
このマッハ円錐の頂点の角度の1/2(すなわち、半頂角)をαとすれば、αは
で示される(M
>1の場合に成り立つ)。このαをマッハ角と呼んでいる。
音波の伝播に関する演習[表計算ファイルのダウンロード]
マッハ数(流速)を変化させて、音波の伝播に与える影響を学習・考察する。
|