Left unary operators
| Operator | Operation | Priority | Example | Mathematical formula |
| abs | absolute value | 6 | abs(x) | |x| |
| sqr | square | 6 | sqr(x) | x2 |
| sqrt | square
root | 6 | sqrt(x) | 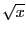 |
| exp | exponential | 6 | exp(x) | ex |
| ln | natural logarithm | 6 | ln(x) | logex |
| log | common logarithm | 6 | log(x) | log10x |
| sin | sine | 6 | sin(x) | sin x |
| cos | cosine | 6 | cos(x) | cos x |
| tan | tangent | 6 | tan(x) | tan x |
| asin | inverse
sine | 6 | asin(x) | sin-1x (
= arcsin
x) |
| acos | inverse
cosine | 6 | acos(x) | cos-1x (
= arccos
x) |
| atan | inverse
tangent | 6 | atan(x) | tan-1x (
= arctan
x) |
| sinh | hyperbolic sine | 6 | sinh(x) | sinh x |
| cosh | hyperbolic cosine | 6 | cosh(x) | cosh x |
| tanh | hyperbolic tangent | 6 | tanh(x) | tanh x |
| asinh | inverse hyperbolic
sine | 6 | asinh(x) | sinh-1x (
= arcsinh
x) |
| acosh | inverse hyperbolic
cosine | 6 | acosh(x) | cosh-1x (
= arccosh
x) |
| atanh | inverse hyperbolic
tangent | 6 | atanh(x) | tanh-1x (
= arctanh
x) |
| cosec | cosecant | 6 | cosec(x) | cosec x ( = 1/sin x) |
| sec | secant | 6 | sec(x) | sec x ( = 1/cos x) |
| cot | cotangent | 6 | cot(x) | cot x ( = 1/tan x) |
| acosec | inverse
cosecant | 6 | acosec(x) | cosec-1
x ( = arccosec x = arcsin 1/x = sin-1 1/x) |
| asec | inverse
secant | 6 | asec(x) | sec-1
x ( = arcsec x = arccos 1/x = cos-1 1/x) |
| acot | inverse
cotangent | 6 | acot(x) | cot-1
x ( = arccot x = arctan 1/x = tan-1 1/x) |
| cosech | hyperbolic cosecant | 6 | cosech(x) | cosech x (=1/sinh x) |
| sech | hyperbolic secant | 6 | sech(x) | sech x (=1/cosh x) |
| coth | hyperbolic cotangent | 6 | coth(x) | coth x (=1/tanh x) |
| acosech | inverse hyperbolic
cosecant | 6 | acosech(x) | cosech-1
x ( = arccosech x = arcsinh 1/x = sinh-11/x) |
| asech | inverse hyperbolic
secant | 6 | asech(x) | sech-1
x ( = arcsech x = arccosh 1/x = cosh-1 1/x) |
| acoth | inverse hyperbolic
cotangent | 6 | acoth(x) | coth-1
x ( = arccoth x = arctanh 1/x = tanh-1 1/x) |
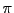 (=3.14159...) in the function, you can use character string "pi".
(=3.14159...) in the function, you can use character string "pi".
 home
home
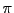 (=3.14159...) in the function, you can use character string "pi".
(=3.14159...) in the function, you can use character string "pi".
 x
x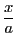
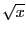
 a
a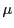 ), p2 : standard deviation(
), p2 : standard deviation(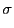 )
)