問題と解答記入エリア
・時間進行とともに変化しない流れを
といい、
時間進行とともに変化する流れを
という。
・圧縮性を考慮しない(圧縮性がない)流れを
といい、
圧縮性を考慮した(圧縮性がある)流れを
という。
 |
|---|
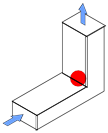
| 図 3次元流れ |
・3次元流れの学習(文章と図について学習したら解答欄にCAを入力する。)
3次元流れとは、実際に我々が生活している空間の流れである。しかし、学習するには複雑で難しく、一般に教科書・問題集にはほとんど取り上げられない。例えば、図の流路(L字型流路)のおいて曲がり部(図の赤丸位置)の流れは相当複雑になると考えられる。
CA
:学生番号下3桁の数字を入力する。
 |
|---|
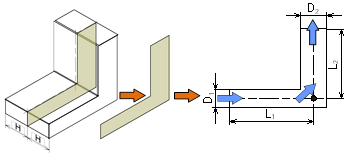
| 図 2次元流れ |
・2次元流れの学習(文章と図について学習したら解答欄にCAを入力する。)
2次元流れとは、例えば、左図の流路において長さ H を流路幅 D よりもはるかに大きく取ってその中央の面を取り出した流れである。H は理想的には∞の長さを持つ。3次元流れと異なり、人間が理解しやすく、流れ模様(流線や速度ベクトル)も比較的容易に描くことができるため、学習目的の数値計算によく用いられる。しかし、この流れでもなお手計算、電卓による計算での見積もりは困難である。また、実験においても取り扱いや考察が容易であるため流れ場を2次元に設定することは少なくない。なお、類似の流れ場に軸対称流れがある。これは、円筒形の流れ場において一つの面を取り出したものである。
CA
:学生番号下3桁の数字を入力する。
 |
|---|
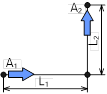
| 図 1次元流れ |
・1次元流れの学習(文章と図について学習したら解答欄にCAを入力する。)
1次元流れとは、図のように流路を中心軸で代表させ、流路の各断面を通過する平均速度を用いて流れを表すものである。一般に流路幅 D に対し、流路長さLは十分に長くなければならない。2,3次元流れのような流れ模様を示すことはできないが、構造が単純であるため、学習計算、(流れを扱う)現場での計算・見積もりによく用いられる。本講義で計算する流れはほとんどがこの1次元流れである。
CA
:学生番号下3桁の数字を入力する。
・以下のリンクページで 流線、流脈線、流跡線の学習を行うこと。
流線、流脈線、流跡線の学習
※ieの場合、
必ず互換機能を切ってください。
(ブラウザの戻るで戻って下さい。)
「リンクページでの操作説明」
学生番号を入力し、流線、流脈線、流跡線いずれかのモードを選択する。
「描画実行」ボタンを押して学習を開始し、「停止」ボタンを押すと
停止後、それぞれのモードに対応する結果数字が表示される。
この結果数字(3つ)をメモして、このページに戻る。
以下の欄に結果数字を入力する。
流線の結果数字
流脈線の結果数字
流跡線の結果数字