問題と解答記入エリア

・図(マノメータ２)においてρ_A＝ρ_Bでその液体を水(20℃)とする。また、上方の流体は油とし、その比重sを0.8とする。hを100mm、h₁をCB(mm)、h₂をCA(mm)とするとき、P_A - P_Bを求めよ。

　










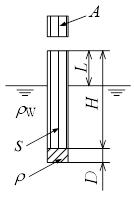
・底面積 A= 500 (mm²)、高さ H=1.0mの直方体の木片がある。この木片を水面(液体は20℃の水)から高さL= CA (mm)だけ突出させて直立させるためにおもり用の鉛（底面積は木片と同じ）を図(浮力１)のように下方に取り付ける。鉛の質量をmとすると、どれほどのmが必要となるか。また、Dはいくらか。ただし、木片の比重をs = (CB-200)*0.001、鉛の密度をρ=11340kg/m³とする。
　ヒント：物体の重さと浮力のつり合いを考える。

m　

D　




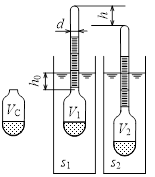
・図(浮力２)のような質量m =5.2gの比重計があり、その円管目盛部の直径はd =4 mmである。また、比重計の円管目盛部を除いた体積をV_Cとする。この比重計を比重s₁と比重s₂の液体に浮かべたときの高低差をhとし、比重計によって液体が排除される体積をそれぞれV₁、V₂とする。s₁=CB*0.001, s₂=s₁-0.05とした場合の高低差hを求めよ。また、h₀ をCA*0.1 (mm)とした場合のV_Cを求めよ。
　ヒント：物体の重さと浮力のつり合いからV₁を求めることができる。V₁に円管断面積×hを加えるとV₂となる。

高低差h　

V_C　

解答清書エリア

空