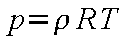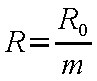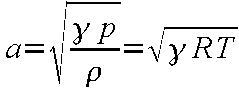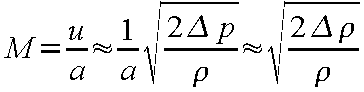●　圧縮性と状態方程式

   一般に流体は圧力が変化すると体積が変化（すなわち密度も変化）する。この性質を圧縮性と呼んでいる。
液体の圧縮性は圧力波のように大きな圧力変化を伴う場合以外は無視される。
一方、気体の圧縮性は大きく、その密度 ρは状態方程式によって求められる。
実在気体ではそれぞれ特有の状態方程式をもつが、普通の圧力ｐ と温度Ｔ  [ T (K)= t (℃) + 273.15] の範囲では、
以下の完全気体の状態方程式が適応できる（R ：気体定数）。

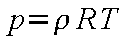(31-1)

　また、普遍気体定数 Ｒ _０ [ Ｒ _０ = 8.3144J/(mol・K) ] と気体定数の関係は以下のようになる。

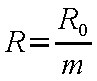(31-2)

ここで、ｍ (g/mol) は１mol あたりの分子の質量（下表参照）を示す。

　※　コラム

　　　気体分子運動論からみる比熱比γについて
　　
　　　気体はその構成原子数に応じて、
　　　　　単原子気体 （ Ar ，He など）　　　　　：　運動の自由度 ν＝３
　　　　　二原子気体 （  O₂ ， N₂ など）　　　　：　運動の自由度 ν＝５　
　　　　　多原子気体 （  CH₄ ， CO₂ など）　　：　運動の自由度 ν＝６
　　　に分類される。
　　　なお、空気は、ほとんどが N₂ と O₂ と構成されるので、二原子気体とみなすことができる。
　　　完全気体の比熱比（定圧比熱／定容比熱）は分子の運動の自由度νを用いて計算することができ、
　　　　定圧比熱　C_p　：　C_p ＝（１＋ν／２）R
　　　　定容比熱　C_ｖ　：　C_ｖ ＝（ν／２）R
　　　　比熱比　　 γ　 ：   γ　＝（ν＋２）／ν
　　　となる。
　　　例えば、二原子気体は γ　＝（５＋２）／５ ＝ ７／５ ＝　１．４ と計算できる。
　　　　　　　

   ●　音速とマッハ数

   気体中に圧力の微小な擾乱を与えると、この変化が四方に伝わる。
この伝ぱ速度を音速という。完全気体の音速 ａ は以下の式で表される（ γ：比熱比 ）。

(31-3)

　また、ある点における流速 ｕ と音速 ａ  の比をマッハ数 Ｍ という。
十分小さいマッハ数に関しては、以下の式の右側のような近似が成り立つ。
すなわち、マッハ数は流体の圧縮性の程度を表している。

(31-4)

　 ●　マッハ数による流れの分類

 (1) 非圧縮性流れ ： 厳密にはＭ  ＝ ０ の流れを示すが、工学上は Ｍ  ＜ 0.3の流れを非圧縮性流れとして取り扱える。
                                   これは、式(31-4)中における Δρ/ρ が Δρ /ρ ＜ 0.05 [5%] に相当している。
 (2) 亜音速流れ    ： Ｍ  ＜ 1の流れを示すが、一般には 0.3  ＜ Ｍ  ＜ 0.8（程度）の流れをいう。
 (3) 遷音速流れ    ： 0.8 ＜ Ｍ  ＜ １.2（程度）の流れをいう。(2)と(4)の間の状態。流れには衝撃波を伴う。
 (4) 超音速流れ    ：  Ｍ  ＞ １ の流れを示すが、一般には1.2 ＜ Ｍ  ＜ 5（程度）の流れをいう。
                                  (4)→(2)の流れに減速される際にはほとんどの場合で衝撃波が発生する。
 (5) 極超音速流れ ： Ｍ  ≧ ５ の流れを示す。この流れでは一般に気体を完全気体として取り扱うことができない。

   ●　衝撃波とは

　飛行機が超音速で飛ぶときや火薬の爆発など短時間に気体が圧縮されるときには極めて強い圧力変化の波が発生する。
気体の状態は断熱的に変化するので、圧力上昇に伴い温度も上昇する。
このような波を圧縮波と呼ぶが、この圧縮波は次第に集中して、その幅が小さくなる傾向を示す。
そして、圧力、温度、密度が不連続的に増加する波面を形成して安定する。この波を衝撃波と呼んでいる。
衝撃波の厚さは非常に薄く μｍ 程度である。

　 ●　演習問題

［問題 １］　空気を完全気体とみなすとき、気温15℃、気圧0.101MPaにおける空気の密度を求めよ。
［問題 ２］　12℃の水素中を伝わる音の速さを求めよ。ただし、水素の比熱比は1.41とする。
［問題 ３］　18℃のヘリウム中を伝わる音の速さを求めよ。ただし、ヘリウムの比熱比は1.67とする。
［問題 ４］　空気中において、ある点の流速が300m/s、温度が30℃であった。この点におけるマッハ数を求めよ。
　　　　　　　ただし、空気の比熱比は1.4とする。

参考文献
(1) 日本機械学会編、「機械工学便覧 流体工学」 (丸善)
(2) 中山泰喜著、「流体の力学」 (養賢堂)
　  

→　戻る