Excelで回帰分析を行う
1. Excelで回帰分析を行う
- 「データ」タブをクリックし、「分析ツール(A)」メニューの中から「回帰分析」を選択し、「回帰分析」の画面の設定を行う。

- 入力元の「入力Y範囲(Y)」には、「Y」のデータが入っているセルの領域
を指定し、「入力X範囲(X)」には、「x」のデータが入っているセルの領域を
指定する。
- 区間推定を行う場合、有意水準(ここでの有意水準は、厳密には信頼係数(1-γ)の値である)95%以外の数値を指定する場合は「有意水準」のところに数値を入力する。
- ラベルも選択する場合は「ラベル(L)」のボックスをクリックする。
- 「出力オプション」は、「出力先」を選択し、セルを指定するか、または、「新規又は次のワークシート(P)」を選択する。
- 「残差」、「正規確率」等の項目は必要に応じて選択する。
- 「OK」ボタンをクリックすると図のような結果が得られる。

- ここで、「係数」の上側が切片αの推定値、下側が回帰係数βの推定値に相当する。これから、y=α+βxという回帰直線の式を求めることができる。
| | 係数 | 標準誤差 | t | P-値 | 下限95% | 上限95% | 下限99% | 上限99% |
| 切片α | -60.71666667 | 7.297271542 | -8.320461465 | 7.08717E-05 | -77.97197192 | -43.46136141 | -86.25334654 | -35.17998679 |
| 回帰係数β | 5.108333333 | 0.322917627 | 15.81930781 | 9.77636E-07 | 4.344754482 | 5.871912185 | 3.978288492 | 6.238378174 |
2. 係数の区間推定
- 回帰分析を行う。
- 回帰分析の結果の表示において、切片α、回帰係数βの値
の表示の「係数」、「標準誤差」、「t」、「P-値」のとなりの数値「下限95%」、「上限95%」の数値が信頼係数95%の区間の数値に相当する。
- 回帰分析の設定画面で有意水準(厳密には信頼係数(1-γ))を指定すると、そのとなりに指定した信頼係数の区間の数値が表示される(上表を参照)。有意水準を指定しないと、信頼係数95%の区間が表示される。
3. 誤差項の分散σ2の区間推定
残差変動(残差二乗和
Σni=1e2i )の値を信
頼係数(1-γ)にしたがって求めた
χ2n-2(1-γ/2)と
χ2n-2(γ/2)の値で割れば、
σ2の信頼区間を求めることができる。ここで、nは
観測数である。
- 回帰分析を行う。
- 残差変動は分散分析表の「残差」と「変動」の交わるところに表示され
た数値である。
- 信頼係数(1-γ)にしたがって、
χ2n-2(1-γ/2)と
χ2n-2(γ/2)の値を計算する。
- σ2の信頼区間は、
残差変動 / χ2n-2(γ/2) ≦
σ2 ≦ 残差変動 / χ2n-2(1-γ/2)
である。
4. 回帰モデルの検定
- 回帰分析を行う。
- 「β=0、すなわち、説明変数xは被説明変数Yに影響を与えない。」という帰無仮説を設定する。
- 「β≠0、すなわち、説明変数xは被説明変数Yに影響を与える」という対立仮説を設定し、両側検定を行う。
- 有意水準γにしたがった棄却域 t < -tn-2(γ/2)、t > tn-2(γ/2)を設定する。
- 回帰分析の結果の表示において、切片と回帰係数の値の表示のところの「係数」、「標準誤差」のとなりの「t」の値(t 値)が棄却域に入っていなければ、帰無仮説は採択され、t値が棄却域に入っていれば、帰無仮説は棄却され、対立仮説が採択される。(t 値の位置で比較)
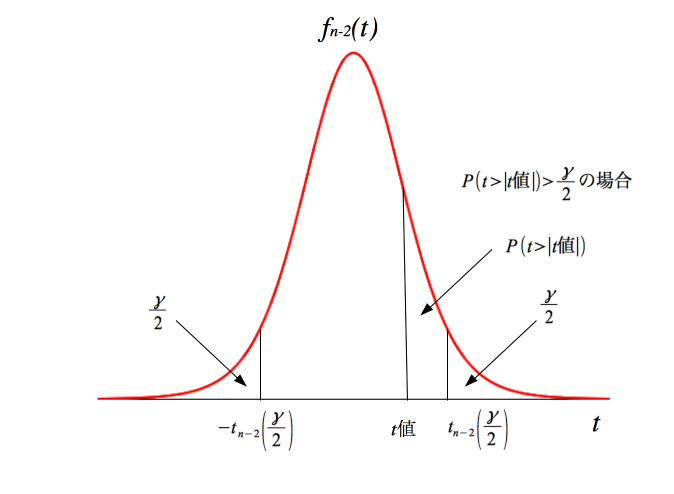
- または、回帰分析の結果の表示において、切片、回帰係数の値の表示のところの「係数」、「標準誤差」、「t」のとなりの「P-値」の数値がγ/2よりも大きければ、帰無仮説は採択され、P-値がγ/2よりも小さければ、帰無仮説は棄却され、対立仮説が採択される。ここで、P-値とは、確率P(t > | t 値 |)の値である。つまり、P(t > | t 値 |) < γ/2であれば、t 値は有意点を超えている(棄却域に入っている)ことになる。(確率の大きさで比較)
その他のOSの場合
- Windows XP以前(Excel97〜2003)の場合、メニューバーから「ツール
(T)」-「分析ツール(D)」を選択する。
- Windows7、Windows
Vista(Excel2007〜)の場合、メニューバーの「データ」を選択し、分析タブの「データ分析」を選択する。
- 以下同じ。
Kazushi Neichi
Department of Business Administration, Tohoku Gakuin University.