Excelでχ2検定(独立性の検定)を行う
準備
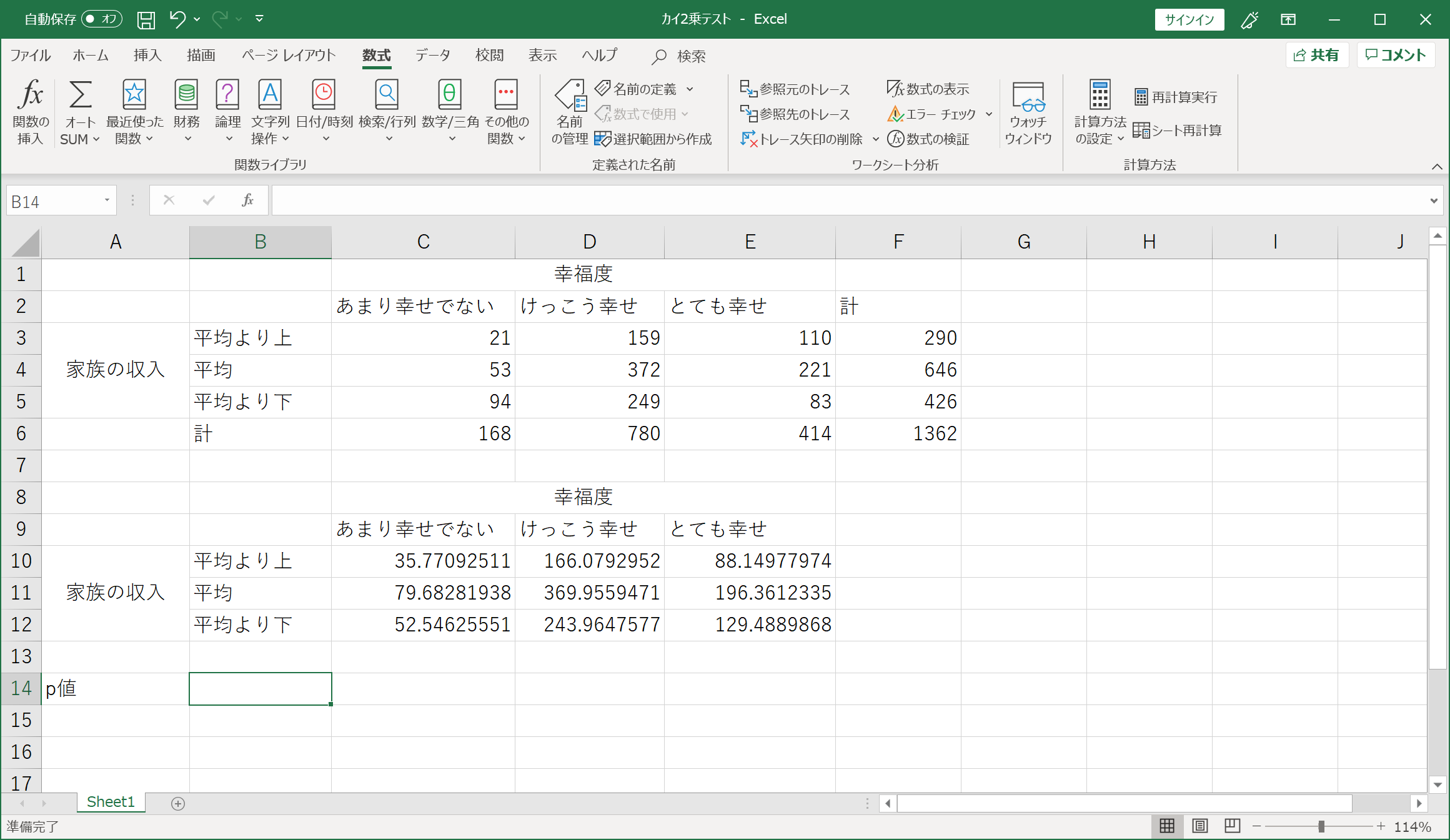
例えば、次のようなクロス表が与えられていたとする。
出典:A. Agresti, "An Introduction to Categorical Data Analysis,
Second Edition", Wiley, 2007
| | 幸福度 |
| あまり幸せでない | けっこう幸せ | とても幸せ | 計 |
| 家族の収入 | 平均より上 | 21 | 159 | 110 | 290 |
| 平均 | 53 | 372 | 221 | 646 |
| 平均より下 | 94 | 249 | 83 | 426 |
| 計 | 168 | 780 | 414 | 1362 |
このクロス表に対してExcelでカイ2乗検定を行う場合、準備として、観測度数
から期待度数の推定値を計算しなければならない。期待度数の推定値Eijは
Eij=fi ⋅ × f⋅ j / n
から計算できる。ここで、fi ⋅は行の周辺度数、
f⋅ jは列の周辺度数、
nは総数である。
このクロス表から期待度数の推定値を計算すると、次のようになる。
期待度数の推定値
| | 幸福度 |
| あまり幸せでない | けっこう幸せ | とても幸せ |
| 家族の収入 | 平均より上 | 35.77 | 166.08 | 88.15 |
| 平均 | 79.68 | 369.96 | 196.36 |
| 平均より下 | 52.55 | 243.96 | 129.49 |
Excelでχ2検定(独立性の検定)を行う
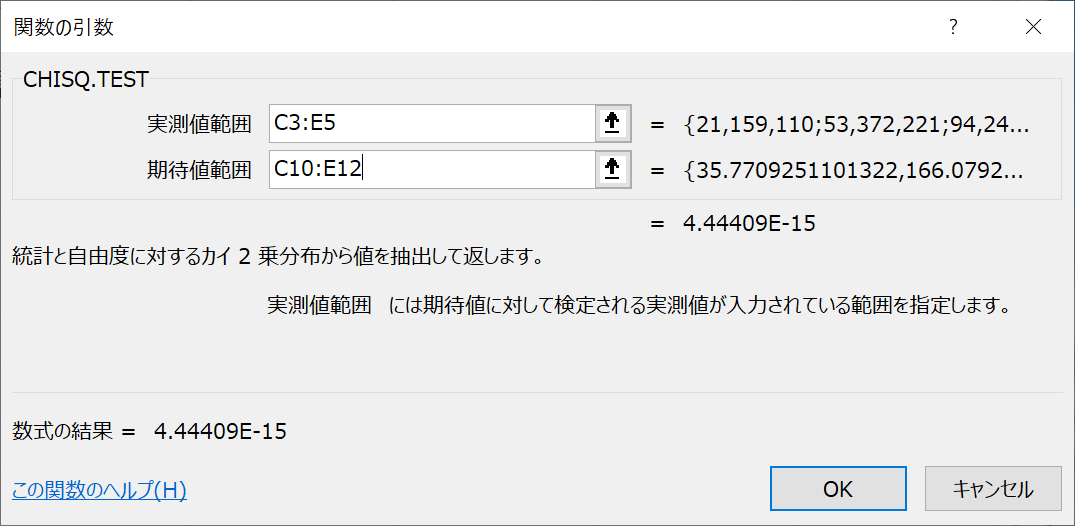
Excelで数式タブをクリックし、その他の関数→統計→CHISQ.TESTを選択し、
- 実測値範囲に観測度数の範囲を指定し、期待値範囲に期待度数の推定値の範囲を指定し、「OK」をクリックする。
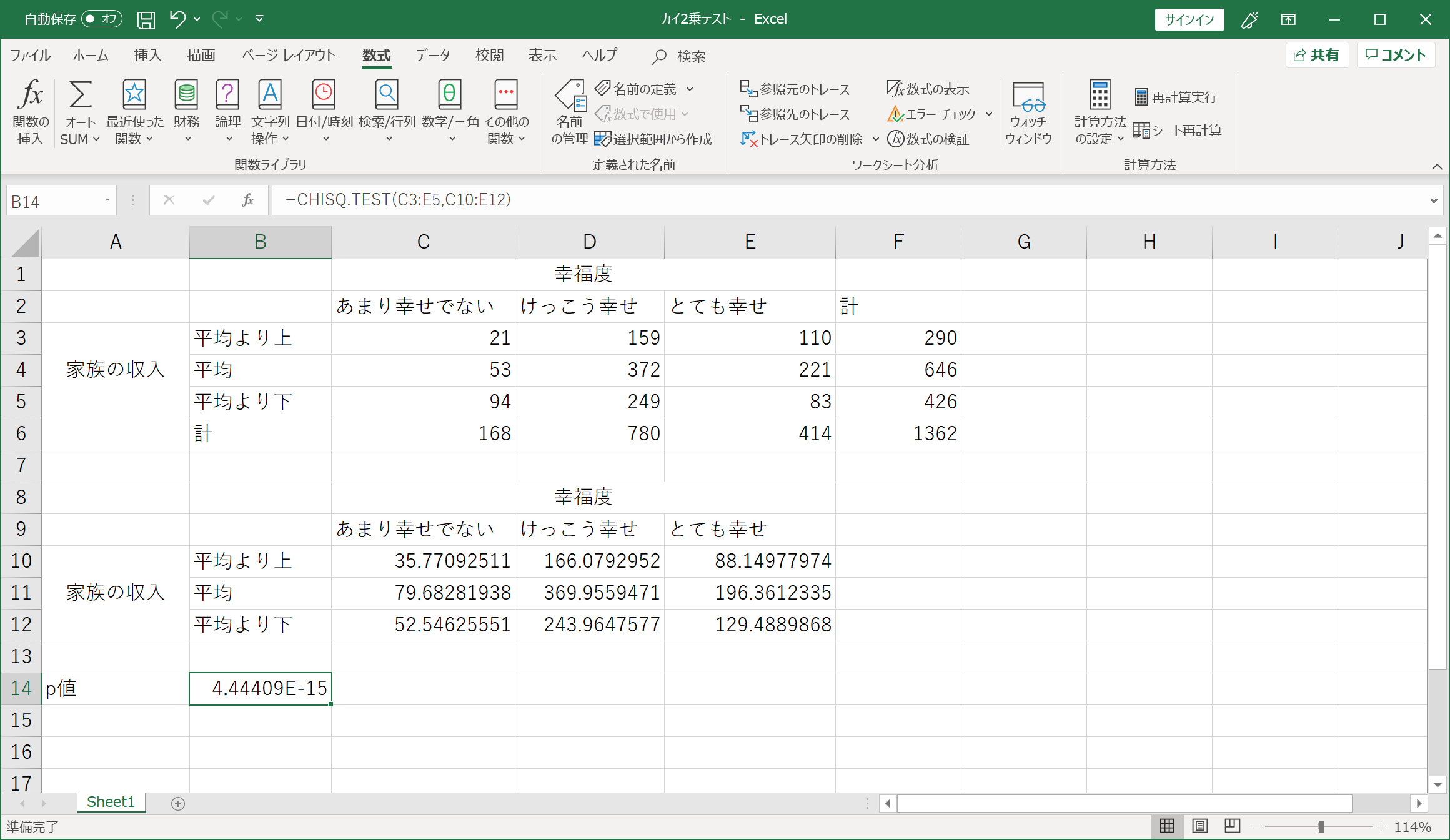
- 自由度(行数-1)×(列数-1)のχ2分布の確率(p-値)が求められる。
自由度(行数-1)×(列数-1)のχ2分布の確率(p-値)が有意水準よりも小さければ、有意である(関係がある)と判定される。
Kazushi Neichi
Department of Business Administration, Tohoku Gakuin University.