


Next: About this document ...
Up: RSA公開鍵暗号方式
Previous: RSA公開鍵暗号方式
花子が、どのようにして秘密鍵(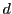 )と公開鍵(
)と公開鍵(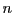 と
と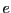 )を導くのかをみ
てみます。
)を導くのかをみ
てみます。
- (1)
- 花子は、互いに素である(1以外に公約数を持たない)2つの非常に大きな素数
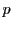 と
と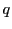 を適当
に選択する。ここで、花子は
を適当
に選択する。ここで、花子は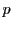 と
と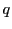 の数値を他人に絶対に秘密
にしなければならない。なぜなら、
の数値を他人に絶対に秘密
にしなければならない。なぜなら、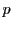 と
と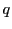 の数値がわかると、
公開鍵
の数値がわかると、
公開鍵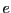 から秘密鍵
から秘密鍵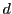 を計算するのは容易であるからである。
を計算するのは容易であるからである。
- (2)
- 1つ目の公開鍵
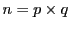 を計算する。
を計算する。
- (3)
- 花子は、
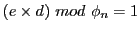 になるような秘密鍵
になるような秘密鍵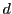 を計算する。ここで、
を計算する。ここで、
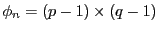 であり、
であり、
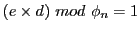 という表記は、「
という表記は、「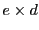 を
を
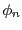 で割った余りが1に等しい」ということを意味する。
で割った余りが1に等しい」ということを意味する。
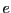 は
は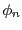 と互いに素になる任意の整数で、2つ目の公開鍵
として使われる。
と互いに素になる任意の整数で、2つ目の公開鍵
として使われる。
このように、花子は、自分の秘密鍵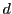 と公開鍵
と公開鍵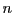 と
と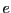 を用意することができ
ます。
を用意することができ
ます。
次に、太郎は、花子から受け取った公開鍵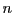 と
と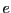 を使って、花子に送るメッセー
ジ
を使って、花子に送るメッセー
ジ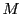 を暗号化して、それを花子に送ります。メッセージの暗号化は、
を暗号化して、それを花子に送ります。メッセージの暗号化は、
という式を使って数学的に暗号化されます。ここで、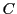 が暗号化されたメッセー
ジになります。
が暗号化されたメッセー
ジになります。
花子の公開鍵で暗号化されたメッセージを送信してもらった花子は、自分の秘密
鍵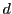 と
と
という式を使って、暗号化されたメッセージ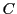 を元のメッセージ
を元のメッセージ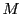 に復号化で
きます。
に復号化で
きます。
実際に簡単な整数を使って、RSA公開鍵暗号方式の例を見てみましょう。
- (1)
- 花子は、互いに素である(1以外に公約数を持たない)2つの素数
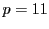 と
と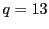 を選択したとする。(
を選択したとする。(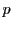 と
と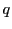 は非常に大きな素数でな
ければならないが、ここでは、話を簡単にするため、小さな素数
を使うことにする。)
は非常に大きな素数でな
ければならないが、ここでは、話を簡単にするため、小さな素数
を使うことにする。)
- (2)
- 1つ目の公開鍵
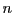 は、
は、
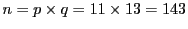 になる。
になる。
- (3)
-
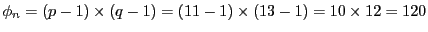 になる。
になる。
- (4)
- ここで、花子は、
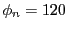 と互いに素になる整数
と互いに素になる整数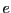 として、
として、
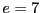 を選択したとする。
を選択したとする。
- (5)
- 次に、花子は、
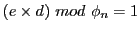 になるような秘密鍵
になるような秘密鍵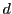 をみつけなければならない。
をみつけなければならない。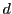 を1から1つずつ増加させながら、
を1から1つずつ増加させながら、
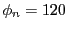 で割った余りが1になるような
で割った余りが1になるような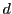 を探していくと、
を探していくと、
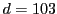 のところで、ちょうど余りが1になる。したがって、
のところで、ちょうど余りが1になる。したがって、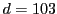 が
得られる。
が
得られる。
これで、花子は、自分の秘密鍵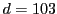 と公開鍵
と公開鍵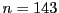 と
と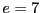 を用意すること
ができました。
を用意すること
ができました。
次に、太郎は、花子にある文字を送信するため、その文字を10進数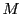 に変換し
ます。ここで、日本語1文字は、16ビットであるので、65,536通りの整数値をと
ることができます。いま、その変換された10進数が
に変換し
ます。ここで、日本語1文字は、16ビットであるので、65,536通りの整数値をと
ることができます。いま、その変換された10進数が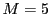 になったとしましょう。太郎は花子から受け取った公開鍵
になったとしましょう。太郎は花子から受け取った公開鍵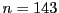 と
と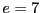 を使って、花子に送信するメッセージ
を使って、花子に送信するメッセージ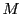 を暗号化します。
を暗号化します。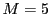 を暗号化すると、
を暗号化すると、
という暗号化されたメッセージ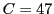 が得られます。暗号化された整数
が得られます。暗号化された整数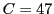 を
送信された花子は、自分の秘密鍵
を
送信された花子は、自分の秘密鍵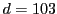 を使って、
を使って、
によって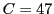 を復号化し、
を復号化し、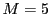 を得ることができます。花子は、この10進数
を得ることができます。花子は、この10進数
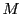 をそれに対応する文字に変換すれば、太郎から送信された文字を読むことが
できます。ここで、
をそれに対応する文字に変換すれば、太郎から送信された文字を読むことが
できます。ここで、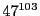 を電卓で計算するわけにはいきません。そこで、
を電卓で計算するわけにはいきません。そこで、
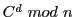 の計算は、かけ算
の計算は、かけ算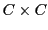 を1回繰り返すごとに
を1回繰り返すごとに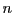 で割った余
りを計算し、その余りに
で割った余
りを計算し、その余りに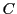 をかけた値を、さらに
をかけた値を、さらに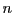 で割った余りを計算するこ
とを(
で割った余りを計算するこ
とを(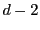 )回繰り返せばよいことと同じになります。
)回繰り返せばよいことと同じになります。
この例では、公開鍵の数値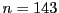 と
と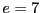 は小さい値なので、秘密鍵
は小さい値なので、秘密鍵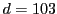 は
簡単に推測できます。
は
簡単に推測できます。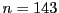 を素因数分解すれば、
を素因数分解すれば、
の3つの場合だけが得られます。これから、
は簡単に推測することができます。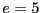 がわかっているので、
がわかっているので、
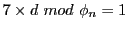 の計算において、
の計算において、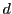 を1から1つずつ増加させなが
ら、
を1から1つずつ増加させなが
ら、
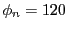 で割った余りが1になるような
で割った余りが1になるような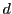 を探していくと、
を探していくと、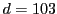 は簡単に得られます。つまり、秘密鍵は簡単に見破られてしまうことになります。
したがって、強い暗号にするためには、公開鍵の数値は非常に大きな数でなけれ
ばなりません。RSA暗号化方式では、1024ビットの公開鍵を使うことが推奨され
ています。
は簡単に得られます。つまり、秘密鍵は簡単に見破られてしまうことになります。
したがって、強い暗号にするためには、公開鍵の数値は非常に大きな数でなけれ
ばなりません。RSA暗号化方式では、1024ビットの公開鍵を使うことが推奨され
ています。



Next: About this document ...
Up: RSA公開鍵暗号方式
Previous: RSA公開鍵暗号方式
Kazushi Neichi
2008-02-05
![]() と
と![]() を使って、花子に送るメッセー
ジ
を使って、花子に送るメッセー
ジ![]() を暗号化して、それを花子に送ります。メッセージの暗号化は、
を暗号化して、それを花子に送ります。メッセージの暗号化は、
![]() と
と
![]() と公開鍵
と公開鍵![]() と
と![]() を用意すること
ができました。
を用意すること
ができました。
![]() に変換し
ます。ここで、日本語1文字は、16ビットであるので、65,536通りの整数値をと
ることができます。いま、その変換された10進数が
に変換し
ます。ここで、日本語1文字は、16ビットであるので、65,536通りの整数値をと
ることができます。いま、その変換された10進数が![]() になったとしましょう。太郎は花子から受け取った公開鍵
になったとしましょう。太郎は花子から受け取った公開鍵![]() と
と![]() を使って、花子に送信するメッセージ
を使って、花子に送信するメッセージ![]() を暗号化します。
を暗号化します。![]() を暗号化すると、
を暗号化すると、
![]() と
と![]() は小さい値なので、秘密鍵
は小さい値なので、秘密鍵![]() は
簡単に推測できます。
は
簡単に推測できます。![]() を素因数分解すれば、
を素因数分解すれば、