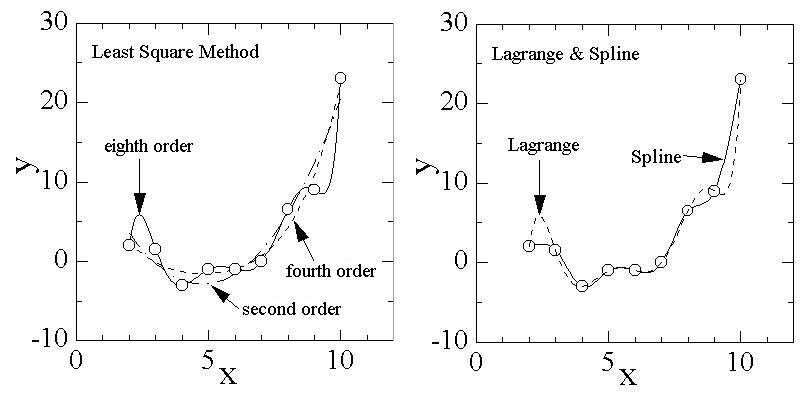
関数近似のサンプルです。

左の図は、9点のプロット点を多項式の最小二乗法で近似しています。
プロット点は、9点ですので、8次式で近似すると、全てのプロット点を通過します。これは、2点は1次式で、3点は2次式でプロット点を全て通過することから推測できますよね。

で・・　みなさんはどう思いますか。一般的には、図のようなばらつきは、測定誤差や、実験条件などによるものですし、データの特性からして、滑らかな変化が妥当であると思われる場合などは、4次式近似あたりが妥当だと思いませんか。

右の図は、ラグランジェの補間公式とスプライン近似です。ラグランジェの補間公式は、プロット点を全て通過する多項式の最小二乗法と同じです。スプライン近似は、いくつかの種類があります。これも、場合によって使い分けるべきでしょう。

で・・・　あらためて・・・
　関数近似は、必ずグラフを描いて見ること。実験条件やデータ特性などを総合的に考慮して選択する必要があります。センスが必要なんですね。